От реальной конструкции к расчётной модели

Практически можно всегда развивать УМЕНИЕ по составлению расчётных схем на ПРОЧНОСТЬ, ЖЁСТКОСТЬ, УСТОЙЧИВОСТЬ и КОЛЕБАНИЯ, используя реальные  конструкции объектов ШИРПОТРЕБА! Выше рассмотрен ПРИМЕР_1  для детских санок! Во-первых, эти объекты общедоступны, а во- вторых, всегда имеются достоверные экспериментальные данные, с которыми можно сравнивать результаты расчётов! Например, рассмотрим обычное пластмассовое ведро (рис.1)!

  

Рис.1

Ведро состоит из двух силовых элементов: ручки и  ёмкости! Нагрузкой при эксплуатации ведра может выступать любой продукт, например, КАПУСТА! Здесь нагрузка достоверна G=100Н будет принята в дальнейшем за базовую эксплуатационную нагрузку! В рассматриваемом случае нагрузка на ёмкость  передаётся по «небольшим» площадкам контакта и может быть смоделирована сосредоточенными силами!

Усилие, прилагаемое к ручке ведра при его эксплуатации  в статических условиях F=G. Ручка в расчётной схеме моделируется кривым брусом круговой формы радиуса  R и постоянным либо переменным поперечным сечением (рис.2).

 

Рис.2

Ёмкость  в расчётной схеме моделируется конической оболочкой, закрытой дном в виде сопряжённой с ней круговой пластинки-мембраны, иногда с рёбрами жёсткости. По широкому краю  у ёмкости имеется  отбортовка  в виде кольца. Ручка на краях имеет консольные  цилиндрические элементы (рис.3), которыми она соединяется через проушины с ёмкостью. Проушины представляют собой небольшие физические тела с круговыми отверстиями. Проушины выполнены заодно целое с отбортовкой и расположены диаметрально. Из описания реальной схемы, очевидно, что наиболее напряжёнными элементами  являются: концевые элементы ручки и проушины.  Рассмотрим следующие расчётные схемы для этих элементов (рис.3).

 

Рис.3

В рассматриваемом случае нагружения, напряжёнными элементами являются так же дно ведра и оболочка ёмкости! Для этих элементов рассмотрим следующие расчётные схемы (рис.4,5).

 

Рис.4. «Жёстко защемлённая» пластинка, нагруженная в центре сосредоточенной силой.

 

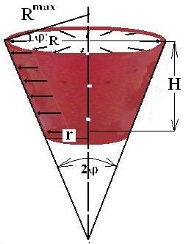
Рис.5. Коническая оболочка, нагруженная избыточным давлением.

Геометрия конической оболочки: R=0.12м; r=0.09м; H=0.28м;

φ = arc tg[(R-r)/H] = arc tg (0.107)→ φ = 6.3⁰ – половина угла конусности;

t = 0.003м – толщина оболочки.

Определение максимальных напряжений в основном силовом элементе.

Максимальные касательные напряжения от перерезывающего усилия Q₀ (рис.3)

τ^max = Q₀/A₀                                                                                    (1)

Q₀ = G/2 = 100Н/2 = 50Н;

A₀ = π∙d²/4 = 3.14∙0.005²/4 =0.2∙ 10^-4 м² – площадь среза концевого элемента;

τ^max = 50Н/0.2∙ 10^-4 м² = 2.5 МПа;

d = 0.005м –диаметр концевых элементов крепления ручки к ёмкости.

Максимальные напряжения изгиба концевого элемента определяем по двум сечениям: сечение элемента справа на рис.3, изгибающий момент M₀ и сечение  элемента слева на рис.3, изгибающий момент М₁. Для определения максимальных напряжений изгиба, необходимо вычислить моменты сопротивления рассматриваемых сечений.

W₀ = 0.1∙d³ =0.1∙0.005³ = 0.0125∙10^-6м³

W₁ = bh²/6 = 0.005∙0.01²/6 = 8.3∙10^-8м³

Изгибающие моменты соответственно равны:

М₀ = P∙c₀  = 50Н∙0.003м = 0.15 Нм

М₁ = Р∙c₁ =  50Н∙0.008м = 0.4 Нм

Максимальные напряжения изгиба:

σ₀ ^max = М₀/ W₀ = 0.15 Нм  / 0.0125∙10^-6м³ = 12МПа                             [2]

σ₁ ^max = М₁/ W₁ = 0.4 Нм / 8.3∙10^-8м³= 4.8МПа

В сечении элемента слева на рис.3. действуют нормальные растягивающие напряжения:

σ_N1 = N₁/A₁ = 50Н/0.01∙0.005 = 1МПа

Известно, что предел прочности для ПЛАСТМАСС изменяется в диапазоне

σ_в = 48-83 МПа.

Коэффициент запаса статической прочности сечения 0:

n_min  = 48/12 = 4

Коэффициент запаса статической прочности сечения 1:

n_min  = 48/5.8 = 8.3

Максимальный изгибающий момент в среднем сечении ручки (рис.2):

M^max = P∙(R-c) = 50∙ (0.15-0.008) = 7.1Нм, где

R = 0.15м; с = с₁ =0.008м

Максимальные напряжения изгиба

σ^max = M^max/ W^min = 7.1Нм / 0.504∙10⁶ = 14МПа, где

W^min = BH²/6 – 2bh²/6 – минимальный момент сопротивления сечения изгибу.

 

Рис. 6. Поперечное сечение 2-2 ручки ведра.

Коэффициент запаса статической прочности сечения2-2:

n_min  = 48/14 = 3.4

Примечания:

1. При эксплуатации ведра в реальных условиях часто происходит разрушение ручки ведра в любом из рассмотренных сечений. Это обусловлено следующими причинами: перегрузка ведра больше нормы (мы здесь приняли условно за норму - нагрузку в 100Н!)
2. Плоская форма ручки неустойчива, происходит поворот сечения 2-2 и кроме изгиба, в сечениях действует крутящий момент! Момент сопротивления сечения 2-2 относительно оси Y существенно меньше W^min, вычисленный относительно оси X.

Проведём оценку напряжённого состояния в пластинке (рис.4)

Согласно [1], наибольший изгибающий момент будет в центре пластинки, где он равняется:

M₁ = M₂ = (3+μ)∙q∙a216 , где                                                            [3]

μ – коэффициент Пуассона;

q = 2Р/πr² = 2∙50Н/3.14∙0.08² ≈ 5кПа – давление на дно ведра;

a  =r = 0.08м – радиус пластинки, моделирующей дно ведра;

M₁ – радиальный изгибающий момент;

M₂ – окружной изгибающий момент.

Максимальные напряжения:

σ^max = 6M^max/t² – где

M^max = (3+0.15)∙5∙0.08216  = 0.0063 кНм/м – максимальный изгибающий момент на единицу ширины радиального или окружного сечения пластинки;

t- Толщина пластинки;

σ^max = 6∙0.0063/0.005² = 1.5 МПа для толщины дна t=5мм;

σ^max = 6∙0.0063/0.003² = 4.2 МПа для толщины дна t=3мм;

Коэффициент запаса статической прочности

n = 48/4.2 >> 1

И, наконец, проведём оценку изгибных напряжений в конической оболочке.

Безмоментные напряжения определяются по формуле:

σ₀ = qR^max/t                                                                                    [4]

Принимаем величину избыточного давления для конической оболочки q=5кПа. Максимальный радиус кривизны оболочка имеет по большому кругу:

R^max = R/Cos(φ) = 0.12/ Cos(6.3⁰) =  0.121м

σ₀ = 5∙0.121/0.003 = 202 кПа (0.2 МПа)

Уровень напряжений безопасный!

Изгибные напряжения в конической оболочке от сосредоточенных сил оценим по модели кольца, нагруженного двумя радиальными силами.

Согласно [2], максимальный изгибающий момент

М^max= PR_ср/π = 50Н∙0.105м/3.14 = 1.67Нм                                  [5]

Момент сопротивления сечения кольца изгибу

W_min = Ht²/6 = 0.28 ∙ 0.003²/6 =0.42∙ 10^-6 м³

Максимальные напряжения изгиба

σ^max = M^max/            W_min = 1.67Нм/0.42∙ 10^-6 м³ ≈ 4МПа

Коэффициент запаса статической прочности

n = 48/ 4 >> 1

Выводы

1. Проведённые прочностные расчёты по нескольким модельным расчётным схемам свидетельствуют о достаточной статической прочности ведра на нормативную нагрузку 100Н.
2. Разные уровни напряжённого состояния для составляющих элементов свидетельствуют о потенциальной возможности дальнейшего увеличения надёжности данной конструкции!
3. Только грамотный инженер расчётчик, умеющий строить расчётные модели, соответствующие реальной конструкции, может принимать ответственные решения по результатам прочностных  расчётов!